"Does Reinforcement Learning Really Incentivize Reasoning Capacity in LLMs Beyond the Base Model?"

This isn't a new intuition, but a nice new set of results.

The paper in question Does Reinforcement Learning Really Incentivize Reasoning Capacity in LLMs Beyond the Base Model? has a lot of discussions underway on if Reinforcement Learning from Verifiable Rewards (RLVR) is actually improving the models we’re training.

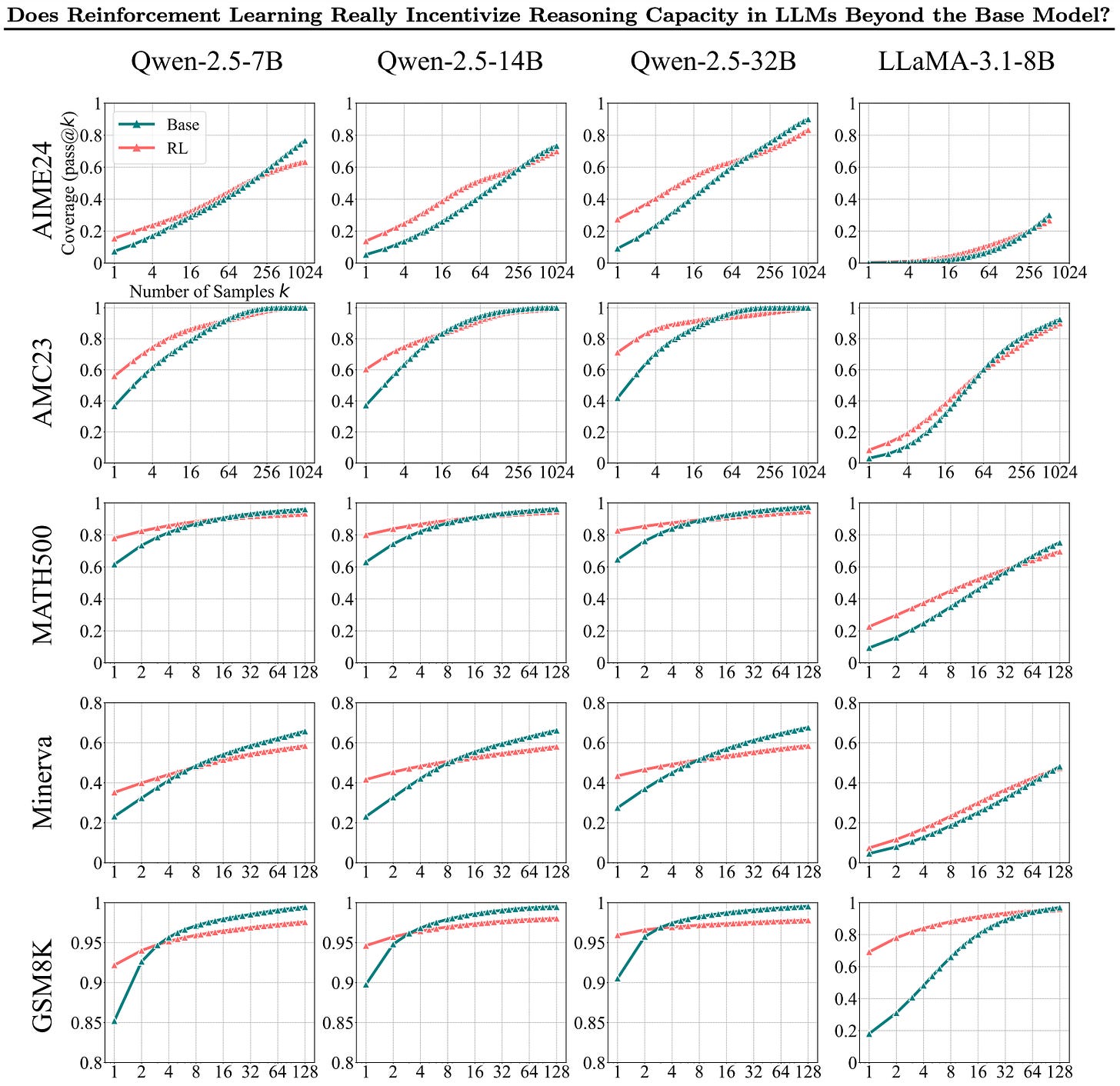
The core figures are the following:

And:

These are all using pass@k as the core metric. Pass@k is the metric that checks to see if the right answer exists in k completions. This is not how practical inference works, but is a good test to see if the model is “in distribution.”

The argument is that as high K, the base models do the same or outperform the RL models. This is cool because it shows that RL reduces the entropy of samples but makes the model more effective at pass@1. We know any post training will reduce the variance in answers and this is a new way to see it. Higher variance will mean more likely to pass the pass@k metric for high k. Honestly, as we get better at RL we should be able to make it induce more exploration, given that’s a core topic of RL’s entire existence, well before language models.

The paper is trying to make you ask: If base models outperform RL trained models, why do we need this RL training?

You should focus on the bottom three rows here which are in-distribution for the RL training data. Second, Qwen is known to be predisposed to learning reasoning so those base models may be stronger. I can’t say a lot more about the base models as that’s an open area of research — what are the right base models for reasoning?

Some are surprised that the base model does so well, but really we’ve been saying for a while that RL training is increasing the probability of correct behaviors — elicitation. With this view, the results align totally with what RLVR should be doing.

There are also some caveats on the work that make it have the usual academic grains of salt. Mostly, they only train on the MATH and GSM8K training sets. While this is great for controlled ablations, it’s not great for showing the fundamental limits of RL training. OpenAI and others have shown that scaling RL is a crucial aspect of it, and with only these narrow training sets that isn’t really possible.

Second, the paper doesn’t have a ton of plots showing the training curves for their models. It’s safe to assume they’re decent because the results look reasonable, but the base model training is much more reliable than the RL training in another paper trying to make a point.

The pass@1 results for RL are extremely promising and should reinforce that RLVR is working. That being said, if we had perfect verifiers — an oracle — we’d never need RLVR in the first place (or post-training really), and we could just use that instead of trying to make the model better. My very first post on inference models made the same point that random sampling with pass@k metrics is important as a baseline for inference scaling!

This isn’t new. This is a nice reminder that there’s no free lunch. We should keep checking how this changes as we:

• Scale RL training to many more prompts, and

• Scale RL to bigger base models.

A final caveat, which I think is minor. These results are all RL-Zero style, i.e. just on the base model with no warm start. DeepSeek and others stated that better performance comes from a warmup with on-policy SFT before RL. This’ll make the RL results above even stronger, where the base model results won’t change.

I’m still optimistic on RL. Come on, don’t go too goldfish, we just got o3 and Gemini 2.5, wonderful models with RL. Still thinking it’s a dead end?